Полезность для игрока Ε в этот момент времени равна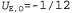

• А если первым ходит игрок О, то складывается ситуация, показанная на рис. 17.9, г. Игрок О из корневой позиции делает ход [q: one; (1-q) : two], после чего игрок Ε выбирает ход с учетом значения д. При этом вознаграждения определяются соотношениями 2gq-3 (1-q) =5q-3 и -3q+4(l-q)=4-7q. Опять-таки на рис. 17.9, е показано, что наилучший ход, который может быть сделан игроком О из корневой позиции, состоит в выборе точки пересечения, следующим образом:

Полезность для игрока Ε в этот момент равна

Теперь известно, что истинная полезность этой игры находится в пределах от -1/12 до -1 /12, т.е. она точно равна -1/12! (Общий вывод состоит в том, что в эту игру лучше играть от имени игрока О, а не Е.) Кроме того, истинная полезность достигается при использовании смешанной стратегии [7/12 : one; 5/12 : two], которой должны придерживаться оба игрока. Такая стратегия называется максиминным равновесием игры и соответствует равновесию Нэша. Обратите внимание на то, что каждая составляющая стратегия в равновесной смешанной стратегии имеет одну и ту же ожидаемую полезность. В данном случае и ход one, и ход two имеют ту же ожидаемую полезность, -1/12, что и сама смешанная стратегия.

Приведенный выше результат для игры в чет и нечет на двух пальцах представляет собой пример общего результата, полученного фон Нейманом: каждая игра с нулевой суммой с двумя игроками имеет максиминное равновесие, если разрешены смешанные стратегии. Кроме того, каждое равновесие Нэша в игре с нулевой суммой представляет собой максиминное равновесие для обоих игроков. Но общий алгоритм поиска максиминных равновесий в играх с нулевой суммой немного сложнее по сравнению с тем, что показано в виде схем на рис. 17.9, д и е. Если количество возможных действий равно л, то смешанная стратегия представляет собой точку в n-мерном пространстве и прямые линии становятся гиперплоскостями. Возможно также, что над некоторыми чистыми стратегиями для второго игрока будут доминировать другие стратегии, так что они перестанут быть оптимальными по отношению к любой стратегии для первого игрока. После удаления всех подобных стратегий (а эту операцию может потребоваться выполнить неоднократно) оптимальным вариантом хода из корневой позиции становится самая высокая (или самая низкая) точка пересечения оставшихся гиперплоскостей. Поиск этого варианта представляет собой пример задачи линейного программирования — максимизации целевой функции с учетом линейных ограничений. Такие задачи могут быть решены с помощью стандартных методов за время, полиномиально зависящее от количества действий (а также формально и от количества битов, используемых для определения функции вознаграждения).